Machine learning for mortals: probabilistic programming with PyMC
by Shashi Gowda (speaking)
Objective
-
Introduction to Probabilistic Programming - a powerful new way of expressing machine learning problems that does not require a rigorous understanding of probability theory or machine learning itself.
-
Learn about Markov chain Monte Carlo - the machinery behind PyMC.
-
Explore some examples which exhibit PP's value in reducing complexity of an implementation, and while at it implement a few common ML algorithms as simple probabilistic programs using PyMC.
-
My hope is that attendees go back knowing about a new tool they can use to easily explore probabilistic models for their data and make hypotheses more fearlessly.
Description
This talk assumes no background in Machine Learning or inference and aims to start from first principles. Distributions and (minimal) jargon thrown in will be explained and a general framework for thinking about inference problems will be shown.
Introduction
The most interesting real-world processes involve uncertainty. Tons of data is amassed everyday from such processes in varied fields: science, engineering, medicine, business, the Internet etc. Expertise in probability theory and machine learning has been essential for programmers to employ computers to model and ask the questions about the process. Probabilistic programming aims to make such modeling accessible to the working programmer with enough domain knowledge, but not necessarily with a thorough knowledge of probability theory or machine learning. Here’s how:
Simulating a random process is easy: you instruct the computer to proceed in the same way as the process--from causes to effects. Inference is the harder, reverse problem: given some evidence about the outcomes observed, the computer needs to infer what configuration of the world could have resulted in the outcomes, and with what certainty. The natural approach to inference is the Bayesian method (grown from the Bayes’ rule). To encode Bayesian inference as a program you will need to do derivations that require strong mathematical background and quickly become mind boggling. What if one could do inference just by creating a plausible simulation of the process?
Monte Carlo techniques let us do exactly that. Answers got with Monte Carlo are approximately equivalent to those from Bayesian inference without the overhead of the abstract thinking.
To estimate the expected value of a function f(x) [where x is a vector of random variables in a probabilistic process], one repeats the experiment N times and notes down the value of the function as observed in each trial. The average of these observations is then returned as the estimated expected value of f. This estimation gets better as N gets larger.
The function f can be all sorts of things. As a simple example, suppose you would like to estimate the probability that a biased coin comes up head. Your function f will be 1 if a trial results in a head, 0 otherwise. Suppose you toss the coin 10000 times and find that it came out heads 4000 times, you can now be fairly certain that the probability of getting heads is around 0.4 (average value of f). One famous example used to illustrate Monte Carlo is a method to estimate the value of Pi. Let a circle of diameter d be inset inside a square of edge d, and N random points be chosen from the square. If K of these points also fall inside the circle, then the ratio of the area of the circle to the square is approximately K/N. But we know that this ratio is equal to Pi x (d^2/4) / d^2 (= Pi/4) and thus can approximate the value of Pi. In this case f could have been 4 if the point falls inside the circle, 0 otherwise.
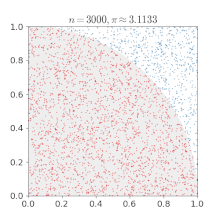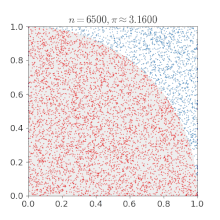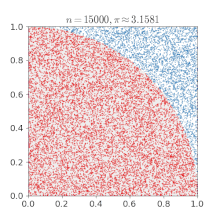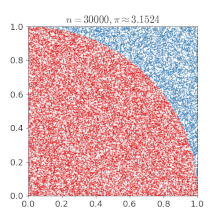
Markov Chain Monte Carlo (MCMC) is an family of MC techniques that are used to estimate integrals, in our case the integrals will be posterior distributions (values of f). You can simply describe the process at hand in terms of well known probability distributions (Bernoulli, Gaussian, Poisson, Uniform etc. -- you need not know the full mathematical details of the distributions, just their high level nature will suffice). Parameters of these distributions can then be inferred by running MCMC on the model leading us to a configuration of the world that would most likely lead to the known evidence (MCMC runs repeated trials incorporating observed data, updating beliefs about these parameters). Here, the function we are estimating, f, can be, for example, the rate of occurrence of coal mine disasters (Poisson process) or say, the probability that a given message is spam, and so on.
Outline of the talk:
- Conceptual overview of the Math
- Random processes
- Probability and probability distributions
- Bayesian inference
- Bayes' theorem
- Conjugate prior distributions
- Examples that show complexity of Bayesian inference
- The Monte Carlo method
- Example: calculating Pi
- Markov Chain Monte Carlo
- Generative models and model fitting with MCMC
- Includes an overview of PyMC
- Examples (Discrete)
- Biased coin toss example - inferring x in Bernoulli(x)
- Judea Pearl’s earthquake alarm (multiple Bernoulli processes)
- Lotka-Volterra predator prey model
- Examples (Common ML algorithms)
- Linear regression
- Naive Bayes
- K-means clustering
- Conclusion
Requirements
A laptop with PyMC and its dependencies installed (optional). Preferably with IPython.
Speaker bio
I am Shashi (Github | Twitter), an autodidact, polyglot python lover, NITK Surathkal batch of '14 alumnus (hopefully).
In the past, I have been a GSoC student for StatusNet (‘10, ‘11), Sahana Eden (‘12) and currently for Julia Language (my project is to create interactive IJulia plots and widgets). I love thinking about code, and sometimes even write some. My latest python project is called phosphene. It’s a library for audio visualization using which I ran visualizations on a handmade disco ball, and other psychedelic peripherals. I work on a data (ECoG) analysis project under Dr. Kaushik Majumdar from ISI, Bangalore. In my free time I evangelize purely functional programming, take Paradigms of Programming classes for juniors, read slow, heavy books and listen to intricate music.
Links
- http://en.wikipedia.org/wiki/Bayesian_inference
- PyMC tutorial http://pymcmc.readthedocs.org/en/latest/tutorial.html
- Probabilistic programming and Bayesian Methods for Hackers (using PyMC) http://nbviewer.ipython.org/github/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers/blob/master/Prologue/Prologue.ipynb
- Why Probabilistic Programming Matters - http://zinkov.com/posts/2012-06-27-why-prob-programming-matters/
- Paper with introduction and state-of-the art inference techniques for infering with probabilistic programs - http://research.microsoft.com/apps/pubs/default.aspx?id=208585
1
▼
Please provide links to your profile and slides and videos from your previous sessions; anything that'll help folks decide if they want to attend your session
2
▼
Hello! This will be the first time I will be giving this talk, and so have no videos. I have written the outline of the talk instead of slides and hoped that will suffice. Will make the actual slideshow if required. My name links to my github and twitter accounts, I should probably make them separate links. Thanks!
1
▼
Hi.. Will you able to cover all these broad topics within 40 mins???
1
▼
I am skeptical. I will rehearse and see what is possible while keeping things effective, these will be the topics I will draw from. I plan to cover Conceptual overview of the Math, and Monte Carlo method in about 10 minutes. Just a quick overview of definitions and illustrative figures while motivating MCMC. (Rigorous understanding is not required for the subsequent portion.)
Introduce Generative models and model fitting with MCMC in 10 minutes and spend 20 minutes on examples. The last 3 examples I do not want to delve into detail, but simply show proof of concept implementations with pointers to code on Github. Does that sound okay? Or do you have suggestions on improving the structure?
Thank you